\(\Large \displaystyle \sigma^2 \)の定義は,
\(\Large \displaystyle V[u_i ] \equiv \sigma^2 \)
でした(ここから).
uiは,
\(\Large \displaystyle Y_i = a_0 + a_1 X_i + u_i \)
です.つまり,真の値,α,β,を用いた場合の,Xi,Yiの残差,ということです.
これとよく似た式が,
\(\Large \displaystyle Y_i = \hat{a_0} + \hat{a_1} X_i + \hat{u_i} \)
各パラメータの違いは,
\(\Large \displaystyle a_0 \) : 切片の真の値
\(\Large \displaystyle a_1 \) : 傾きの真の値
\(\Large \displaystyle u_i \) : Xiを与えた場合のYiと真の値との残差
\(\Large \displaystyle \hat{a_0} \) : 切片の推定値
\(\Large \displaystyle \hat{a_1} \) : 傾きの推定値
\(\Large \displaystyle \hat{u_i} \) : Xiを与えた場合のYiと推定値との残差
となります.
問題は,
我々は真の値,α,β,を知ることはできない
あくまで,推定値,\(\Large \displaystyle \hat{a_0}, \hat{a_1} \) のみ,推定できる
つまり,
uiはわからない,\(\Large \displaystyle \hat{u_i} \) のみ,計算できる
ということです.
なので
\(\Large \displaystyle V[u_i ] \equiv \sigma^2 \),
を完全に計算することはできない(はず)です.
・エクセルでの推定
では,実際のソフトではどのような計算をしているのでしょうか?
代表例としてエクセル,を調べてみます.
こちらと同じデータで考えていきます.
| i | \( X_i \) | \( Y_i \) |
| 1 | 5 | 4 |
| 2 | 1 | 1 |
| 3 | 3 | 1 |
| 4 | 2 | 3 |
| 5 | 4 | 4 |
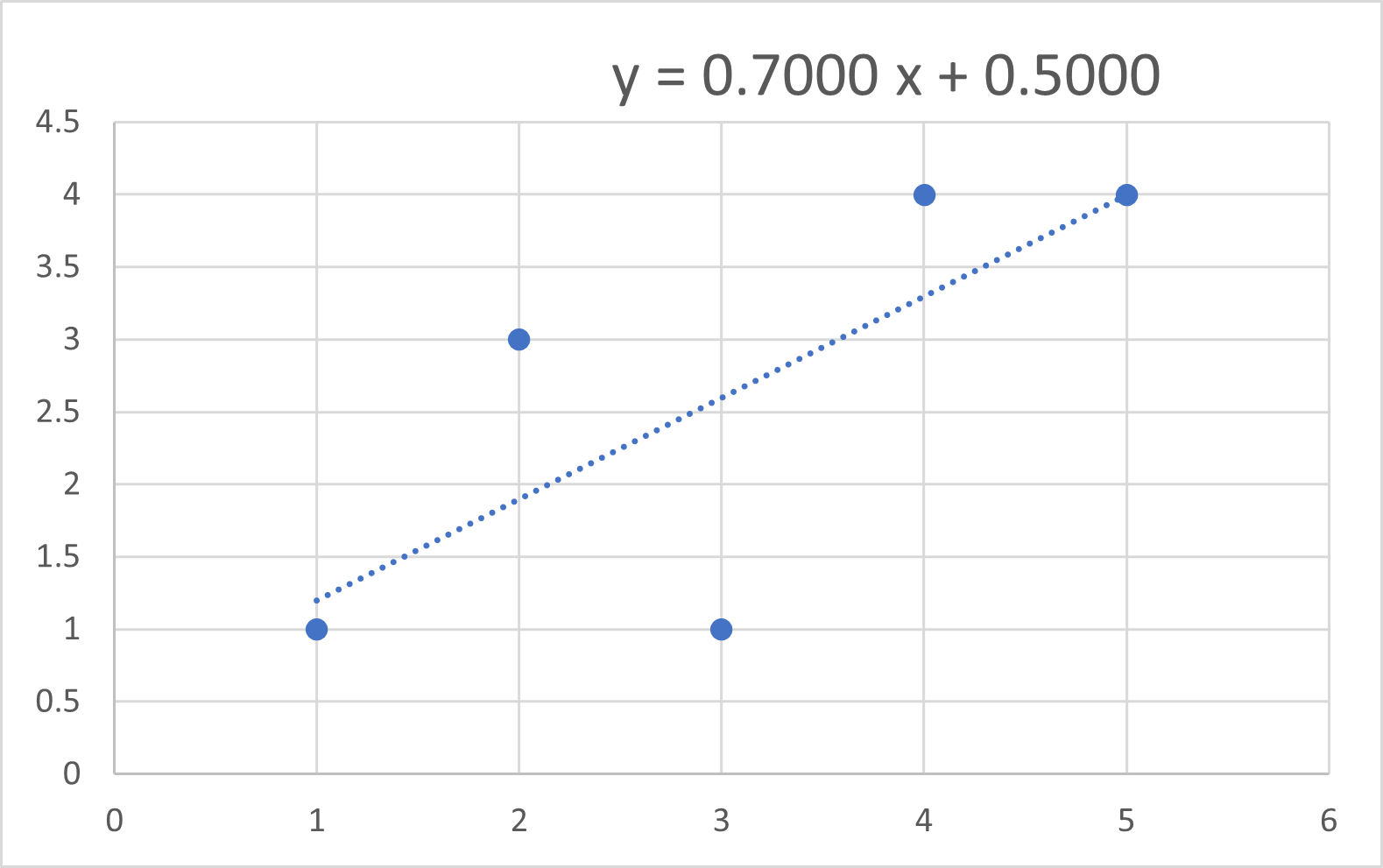
エクセルで 近似すると,

となり,
傾き : 0.70
切片 : 0.50
となります.また,”データ”→”データ分析”→”回帰分析”,から,
| 概要 | ||||||||
| 回帰統計 | ||||||||
| 重相関 R | 0.729800449 | |||||||
| 重決定 R2 | 0.532608696 | |||||||
| 補正 R2 | 0.376811594 | |||||||
| 標準誤差 | 1.197219 | |||||||
| 観測数 | 5 | |||||||
| 分散分析表 | ||||||||
| 自由度 | 変動 | 分散 | 観測された分散比 | 有意 F | ||||
| 回帰 | 1 | 4.9 | 4.9 | 3.41860465 | 0.161593686 | |||
| 残差 | 3 | 4.3 | 1.43333333 | |||||
| 合計 | 4 | 9.2 | ||||||
| 係数 | 標準誤差 | t | P-値 | 下限 95% | 上限 95% | 下限 95.0% | 上限 95.0% | |
| 切片 | 0.5 | 1.25565388 | 0.3981989 | 0.71712901 | -3.496051052 | 4.496051052 | -3.4960511 | 4.49605105 |
| X 値 1 | 0.7 | 0.37859389 | 1.8489469 | 0.16159369 | -0.504854726 | 1.904854726 | -0.5048547 | 1.90485473 |
と係数の推定値,さらには標準誤差が見積もられています.
とりあえず,\(\Large \displaystyle \hat{u_i} \),を計算してみましょう.
| i | \( X_i \) | \( Y_i \) |
\( X_i - \bar{X} \) | \( \hat{a_0} + \hat{a_1} X_i \) | \( \hat{u_i} \) |
| 1 | 5 | 4 | 2 | 4 | 0 |
| 2 | 1 | 1 | -2 | 1.2 | -0.2 |
| 3 | 3 | 1 | 0 | 2.6 | -1.6 |
| 4 | 2 | 3 | -1 | 1.9 | 1. |
| 5 | 4 | 4 | 1 | 3.3 | 0.7 |
| 平均 | 3 | ||||
| 二乗和 | 10 | 4.3 |
・傾きの推定値,\(\Large \displaystyle \hat{a_1} \), の分散
傾きの推定値,\(\Large \displaystyle \hat{a_1} \), の分散は,
\(\Large \displaystyle V \left[\hat{a_1} \right] = \sigma^2 \sum_{i=1}^{n} \omega_i^2
= \frac{\sigma^2 }{\sum_{i=1}^{n} \left( X_i - \bar{X} \right)^2}\)
なので,もし,σを\(\Large \displaystyle \hat{u_i} \),から求めてみると,
\(\Large \displaystyle V \left[\hat{a_1} \right] = \frac{4.3 }{10} = 0.43 \)
標準偏差は,
\(\Large \displaystyle SD \left[\hat{a_1} \right] = \sqrt{ V \left[\hat{a_1} \right]} = \sqrt{ 0.43} = 0.6557\)
エクセルでの推定は,”標準誤差”,ですので,データ数,\(\Large \displaystyle \sqrt{ n-1} \),で割る必要がありますが,ここでは,参考文献,によると,
uiの分散,σ2の不変推定量を,
\(\Large \displaystyle \color{red}{\frac{\sum_{i=1}^n u_i^2}{自由度}} \),
自由度 = 標本数(n) ー 推定すべき係数値の数(2) = n-2
ということのようです(切片と傾きだから2だと思いますが....ちゃんと理解していないかもしれません....)
なので,標準偏差を,\(\Large \displaystyle \sqrt{ n-2} \),で割ると,
\(\Large \displaystyle SE \left[\hat{a_1} \right] = \frac{SD \left[\hat{a_1} \right]}{ \sqrt{n-2}}= \frac{\sqrt{ 0.43}}{\sqrt{3}} = 0.3786\)
と一致します.
・切片の推定値,\(\Large \displaystyle \hat{a_0} \), の分散
同様に,切片の推定値,\(\Large \displaystyle \hat{a_0} \), の分散は,
\(\Large \displaystyle V \left[ \hat{a_0} \right] = \sigma^2 \frac{ \sum_{i=1}^{n} X_i^2 }{n \sum_{i=1}^{n} \left( X_i - \bar{X} \right)^2} \)
なので,もし,σを\(\Large \displaystyle \hat{u_i} \),から求めてみると,
\(\Large \displaystyle V \left[\hat{a_0} \right] = \frac{4.3 \times 55 }{5 \times 10} = 4.73 \)
標準偏差は,
\(\Large \displaystyle SD \left[\hat{a_0} \right] = \sqrt{ V \left[\hat{a_0} \right]} = \sqrt{ 4.73} = 2.1748\)
標準偏差を,\(\Large \displaystyle \sqrt{ n-2} \),で割ると,
\(\Large \displaystyle SE \left[\hat{a_0} \right] = \frac{SD \left[\hat{a_0} \right]}{ \sqrt{n-2}}= \frac{\sqrt{ 2.1748}}{\sqrt{3}} =1.25565 \)
ですので,
\(\Large \displaystyle \sigma^2 = \frac{E \left[ \sum_{i=1}^n \hat{u_i}^2 \right]}{n-2} = s^2 \)
となることになります,ここで,s2は母分散 σ2の不偏推定量と呼ぶ(らしい)です.
次ページに本当にそうなるかを検討していきたいと思います.